Subtree of Another Tree

---

Subtree of Another Tree: Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

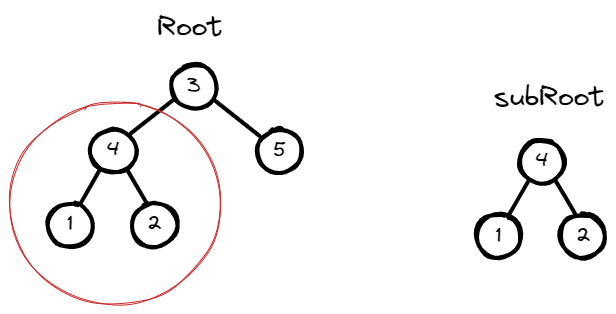
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

---

Example 2:

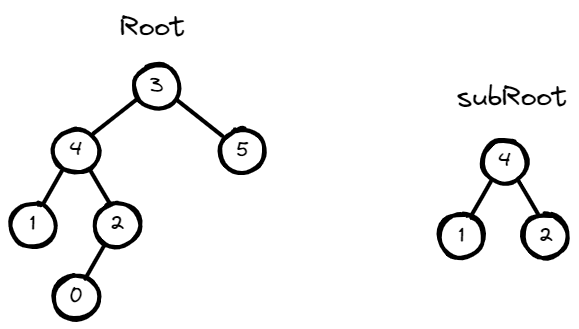
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

---

Constraints:

• The number of nodes in the root tree is in the range [1, 2000].
• The number of nodes in the subRoot tree is in the range [1, 1000].
• -10^4 <= root.val <= 10^4
• -10^4 <= subRoot.val <= 10^4

---

Try this Problem on your own or check similar problems:

1. Same Tree
2. Count Univalue Subtrees
3. Most Frequent Subtree Sum

Solution:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null || subRoot == null) return root == subRoot;
        return isSameTree(root, subRoot) ||
                    isSubtree(root.left, subRoot) ||
                    isSubtree(root.right, subRoot);
    }

    private boolean isSameTree(TreeNode p, TreeNode q) {
        return helper(p, q);
    }

    private boolean helper(TreeNode p, TreeNode q){
        if(p == null || q == null) return p == q;
        return p.val == q.val && helper(p.left, q.left) && helper(p.right, q.right);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} subRoot
 * @return {boolean}
 */
var isSubtree = function (root, subRoot) {
  if (root === null || subRoot === null) return root === subRoot;
  return (
    isSameTree(root, subRoot) ||
    isSubtree(root.left, subRoot) ||
    isSubtree(root.right, subRoot)
  );
};

function isSameTree(p, q) {
  return helper(p, q);
}

function helper(p, q) {
  if (p === null || q === null) return p === q;
  return p.val === q.val && helper(p.left, q.left) && helper(p.right, q.right);
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if root is None or subRoot is None:
            return root is subRoot
        return self.isSameTree(root, subRoot) or self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)

    def isSameTree(self, p, q):
        return self.helper(p, q)

    def helper(self, p, q):
        if p is None or q is None:
            return p == q
        return p.val == q.val and self.helper(p.left, q.left) and self.helper(p.right, q.right)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (root == nullptr || subRoot == nullptr)
            return root == subRoot;
        return isSameTree(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }

private:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        return helper(p, q);
    }

    bool helper(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr)
            return p == q;
        return p->val == q->val && helper(p->left, q->left) && helper(p->right, q->right);
    }
};

---

Time/Space Complexity:

• Time Complexity: O(n*m)
• Space Complexity: O(n)

---

Explanation:

Time complexity is O(n\*m) respectively the number of nodes in root tree and number of nodes in subRoot since for each of the nodes in root we check if it matches with the subRoot using the Same Tree solution. If we don't find a match in root node check left and right subtree. If we have either root == null or subRoot == null, we have match only if they both equal to null so we check for equality. The space complexity in worst case is proportional to the number of nodes in the root tree, since we can have left or right skewed tree and the recursion stack in that case would be of size n.